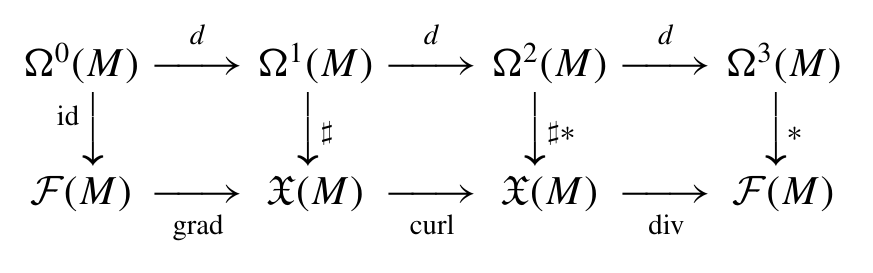1.0.4 Preliminares MatemáticasUniversidade Federal de Campina Grande
Figure 1: Carl Friedrich Gauss (1777-1855), Bernhard Riemann (1826-1866), Élie Cartan (1869-1951), Henri Poincaré (1854-1912)
Unidade: Preliminares MatemáticosGeometria DiferencialVetores e Tensores Tensores isotrópicos Coordenadas Ortogonais Interlúdio: formas diferenciais Operadores Diferenciais Operadores Diferenciais em 3 dimensões Teorema de stokes para formas diferenciais Análise MatemáticaDistribuições Teorema de Helmholtz Função de Green, Problema de Sturm Liouville e Transformadas Integrais. Laplaciano em Coordenadas Esféricas Geometria Diferencial ¶ Métrica de Minkowsky:
η μ ν = d i a g ( + 1 , − 1 , − 1 , − 1 ) \eta_{\mu\nu} = \mathrm{diag}(+1, -1, -1, -1) η μν = diag ( + 1 , − 1 , − 1 , − 1 ) Sistema de Unidades: SI Ocasionalmente usaremos o sistema de unidades natural:
c = 1 , G = 1 , ℏ = 1 c=1,\; G=1,\; \hbar=1\; c = 1 , G = 1 , ℏ = 1 Em uma expressão usando componentes de objetos multilineares (vetores, tensores...), sempre que um índice aperecer duas vezes subentende-seuma soma neste índice sobre o número de dimensões do objeto. Embora existam expressões corretas com um índice repetido mais do que 2 vezes, este é um caso ultra-excepcional. Se você pensar em fazer isto, provavelmente tem um erro no seu cálculo. Índices de soma são chamados de índices mudos e a letra que se usa para designá-los pode ser alterada livremente. Igualdades devem ter os mesmos conjuntos de índices livres, independentemente dos índices mudos. Tensores Isotrópicos (em 3D) ¶ δ i j = [ 0 i ≠ j 1 i = j \delta_{ij} = \left[
\begin{array}{ll}
0 & i\ne j \\
1 & i=j \\
\end{array}
\right. δ ij = [ 0 1 i = j i = j ϵ i 1 ⋯ i d = { + 1 se { i i } e ˊ uma permuta c ¸ a ˜ o par de ( 1 , 2 , 3 ⋯ d ) − 1 se { i i } e ˊ uma permuta c ¸ a ˜ o ı ˊ mpar de ( 1 , 2 , 3 ⋯ d ) 0 se quaisquer ı ˊ ndices s a ˜ o repetidos \epsilon_{i_1 \cdots i_d} =
\begin{cases}
+1 & \text{se $\{i_i\}$ é uma permutação par de $(1, 2, 3\cdots d)$} \\
-1 & \text{se $\{i_i\}$ é uma permutação ímpar de $(1, 2, 3\cdots d)$} \\
0 & \text{se quaisquer índices são repetidos}
\end{cases} ϵ i 1 ⋯ i d = ⎩ ⎨ ⎧ + 1 − 1 0 se { i i } e ˊ uma permuta c ¸ a ˜ o par de ( 1 , 2 , 3 ⋯ d ) se { i i } e ˊ uma permuta c ¸ a ˜ o ı ˊ mpar de ( 1 , 2 , 3 ⋯ d ) se quaisquer ı ˊ ndices s a ˜ o repetidos Um tensor é dito isotrópico se a sua representação em coordenadas é a mesma para todos os sistemas de coordenadas que podm ser obtidos por rotações.
É trivial observar que os escalares são isotrópicos e o único vetor isotrópico é o vetor nulo.
Para objetos tensoriais de posto 2 começamos a encontrar objetos não triviais. Considere uma matriz A A A
onde R R R
R = e ω ⋅ L R T = R − 1 = e − ω ⋅ L e B C e − B = ∑ 1 n ! [ … [ [ [ C , B ] , B ] , B ] … ] ⇒ [ ω ⋅ L , A ] = 0 ω ⋅ L = ( 0 − z y z 0 − x − y x 0 ) \begin{align}
R &= e^{\mathbb{\omega} \cdot \mathbb{L}} \\
R^T &= R^{-1} = e^{-\mathbb{\omega} \cdot \mathbb{L}} \\
e^{B} C e^{-B} &= \sum\frac{1}{n!}[\ldots[[[C, B], B],B]\ldots] \Rightarrow \\
[\mathbb{\omega} \cdot \mathbb{L}, A] &= 0 \\
\mathbb{\omega} \cdot \mathbb{L} &=
\begin{pmatrix}
0 & -z & y \\
z & 0 & -x \\
-y & x & 0
\end{pmatrix}
\end{align} R R T e B C e − B [ ω ⋅ L , A ] ω ⋅ L = e ω ⋅ L = R − 1 = e − ω ⋅ L = ∑ n ! 1 [ … [[[ C , B ] , B ] , B ] … ] ⇒ = 0 = ⎝ ⎛ 0 z − y − z 0 x y − x 0 ⎠ ⎞ Portanto a única matriz isotrópica (tensor de posto 2) é proporcional a δ i j \delta_{ij} δ ij
Para construir um invariante com posto três é necessário usar a álgebra dos geradores, vamoas omitir os detalhes e apenas enunciar de ϵ i j k \epsilon_{ijk} ϵ ijk
e ^ i ⋅ e ^ j = δ i j δ i i = d δ i j = ϵ i j k = 0 [ A × B ] i = ϵ i j k A j B j ϵ i j k ϵ i j k = 6 d e t A = ϵ i j k C i 1 C j 2 C k 3 ϵ l m n d e t A = ϵ i j k C i l C j m C k n ϵ i j k ϵ l m n = ∣ δ i l δ i m δ i n δ j l δ j m δ j n δ k l δ k m δ k n ∣ ϵ i j k ϵ i m n = δ j m δ k n − δ j n δ k m \begin{align}
\hat e_i \cdot \hat e_j &= \delta_{ij} \\
\delta_{ii} &= d \\
\delta_{ij} &= \epsilon^{ijk} = 0 \\
[A \times B]^i &= \epsilon^{ijk} A_j B_j \\
\epsilon^{ijk}\epsilon_{ijk} &= 6 \\
\mathrm{det} A &= \epsilon_{ijk}C_{i1}C_{j2}C_{k3} \\
\epsilon_{lmn}\mathrm{det} A &= \epsilon_{ijk}C_{il}C_{jm}C_{kn} \\
\epsilon_{ijk} \epsilon_{lmn} &= \begin{vmatrix}
\delta_{il} & \delta_{im} & \delta_{in} \\
\delta_{jl} & \delta_{jm} & \delta_{jn} \\
\delta_{kl} & \delta_{km} & \delta_{kn}
\end{vmatrix}\\
\epsilon_{ijk} \epsilon_{imn} &= \delta_{jm}\delta_{kn} - \delta_{jn}\delta_{km}
\end{align} e ^ i ⋅ e ^ j δ ii δ ij [ A × B ] i ϵ ijk ϵ ijk det A ϵ l mn det A ϵ ijk ϵ l mn ϵ ijk ϵ imn = δ ij = d = ϵ ijk = 0 = ϵ ijk A j B j = 6 = ϵ ijk C i 1 C j 2 C k 3 = ϵ ijk C i l C jm C kn = ∣ ∣ δ i l δ j l δ k l δ im δ jm δ km δ in δ jn δ kn ∣ ∣ = δ jm δ kn − δ jn δ km Operador Diferenciais em Coordenadas Cartesianas ¶ O gradiente de uma função escalar f : R 3 → R f:\mathbb{R}^3 \to \mathbb{R} f : R 3 → R f f f
∇ f ( x , y , z ) = ( ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z ) . \nabla f(x,y,z) \;=\;
\left(
\frac{\partial f}{\partial x}, \;
\frac{\partial f}{\partial y}, \;
\frac{\partial f}{\partial z}
\right). ∇ f ( x , y , z ) = ( ∂ x ∂ f , ∂ y ∂ f , ∂ z ∂ f ) . Definição como limite :f f f
∇ f ( r ) = lim V → 0 1 V ∫ ∂ V f ( r ) n ^ d S , \nabla f(\mathbf{r}) \;=\;
\lim_{V \to 0} \frac{1}{V} \int_{\partial V} f(\mathbf{r}) \, \hat{n} \, dS, ∇ f ( r ) = V → 0 lim V 1 ∫ ∂ V f ( r ) n ^ d S , onde V V V r = ( x , y , z ) \mathbf{r}=(x,y,z) r = ( x , y , z ) ∂ V \partial V ∂ V n ^ \hat{n} n ^
O divergente de um campo vetorial F : R 3 → R 3 \mathbf{F}:\mathbb{R}^3 \to \mathbb{R}^3 F : R 3 → R 3
∇ ⋅ F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z . \nabla \cdot \mathbf{F} \;=\;
\frac{\partial F_x}{\partial x} +
\frac{\partial F_y}{\partial y} +
\frac{\partial F_z}{\partial z}. ∇ ⋅ F = ∂ x ∂ F x + ∂ y ∂ F y + ∂ z ∂ F z . Definição como limite :
∇ ⋅ F ( r ) = lim V → 0 1 V ∫ ∂ V F ⋅ n ^ d S . \nabla \cdot \mathbf{F}(\mathbf{r}) \;=\;
\lim_{V \to 0} \frac{1}{V}
\int_{\partial V} \mathbf{F} \cdot \hat{n} \, dS. ∇ ⋅ F ( r ) = V → 0 lim V 1 ∫ ∂ V F ⋅ n ^ d S . O rotacional de um campo vetorial F : R 3 → R 3 \mathbf{F}:\mathbb{R}^3 \to \mathbb{R}^3 F : R 3 → R 3
∇ × F = ( ∂ F z ∂ y − ∂ F y ∂ z , ∂ F x ∂ z − ∂ F z ∂ x , ∂ F y ∂ x − ∂ F x ∂ y ) . \nabla \times \mathbf{F} \;=\;
\left(
\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}, \;
\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}, \;
\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}
\right). ∇ × F = ( ∂ y ∂ F z − ∂ z ∂ F y , ∂ z ∂ F x − ∂ x ∂ F z , ∂ x ∂ F y − ∂ y ∂ F x ) . Definição como limite :
∇ × F ( r ) = lim A → 0 1 A ∫ ∂ A F ⋅ d r , \nabla \times \mathbf{F}(\mathbf{r}) \;=\;
\lim_{A \to 0} \frac{1}{A}
\int_{\partial A} \mathbf{F} \cdot d\mathbf{r}, ∇ × F ( r ) = A → 0 lim A 1 ∫ ∂ A F ⋅ d r , onde A A A r \mathbf{r} r ∂ A \partial A ∂ A
De um ponto de vista mnemônico, podemos construir o operador nabla :
∇ = e i ∂ ∂ x i ,
\nabla = e_i \frac{\partial}{\partial x^i}, ∇ = e i ∂ x i ∂ ,
com o qual escrevemos, exclusivamente para coordenadas cartesianas:
∇ f = ∂ f ∂ x i e i gradiente ∇ ⋅ A ⃗ = ∂ i A i divergente [ ∇ × A ⃗ ] i = ϵ i j k ∂ j A k rotacional \begin{aligned}
\nabla f & = \frac{\partial f}{\partial x^i} e_i & \quad \textbf{gradiente}\\
\nabla \cdot \vec{A} &= \partial_i A^i & \quad \textbf{divergente}\\
[\nabla \times \vec{A}]_i & = \epsilon_{ijk} \partial^j A^k & \quad \textbf{rotacional}
\end{aligned} ∇ f ∇ ⋅ A [ ∇ × A ] i = ∂ x i ∂ f e i = ∂ i A i = ϵ ijk ∂ j A k gradiente divergente rotacional Mudanças de Coordenadas ¶ Considere agora um novo sistema de coordenadas locais não-cartesiano ( ξ 1 , ξ 2 , ξ 3 ) (\xi^1, \xi^2, \xi^3) ( ξ 1 , ξ 2 , ξ 3 )
e i ′ = ∂ r ⃗ ∂ ξ i e i ′ = ∂ x j ∂ ξ i e j = J j i e j \begin{aligned}
e_i'&= \frac{\partial
\vec{r}}{\partial \xi^i}\\
e_i' &= \frac{\partial x^j}{\partial \xi^i} e_j = J^j{}_i e_j
\end{aligned} e i ′ e i ′ = ∂ ξ i ∂ r = ∂ ξ i ∂ x j e j = J j i e j Um vetor é um objeto geométrico invariante por mudanças de coordenadas, logo
X = X i e i = X j ′ e j ′ ⇒ X j ′ = ∂ ξ j ∂ x i X i = J − 1 i j X i \begin{aligned}
X &= X^i e_i = {X^j}' e_j' \Rightarrow \\
{X^j}' &= \frac{\partial \xi^j}{\partial x^i} X^i = {J^{-1}}_i^jX^i
\end{aligned} X X j ′ = X i e i = X j ′ e j ′ ⇒ = ∂ x i ∂ ξ j X i = J − 1 i j X i Coordenadas Curvilíneas Ortogonais ¶ Relação com Cartesianas
x = r cos θ , y = r sin θ , r ≥ 0 , θ ∈ [ 0 , 2 π ) . x = r\cos\theta,\qquad y = r\sin\theta,\qquad r\ge 0,\ \theta\in[0,2\pi). x = r cos θ , y = r sin θ , r ≥ 0 , θ ∈ [ 0 , 2 π ) . Base ortonormal
e ^ r = ( cos θ , sin θ ) , e ^ θ = ( − sin θ , cos θ ) . \hat{\mathbf e}_r=(\cos\theta,\sin\theta),\quad
\hat{\mathbf e}_\theta=(-\sin\theta,\cos\theta). e ^ r = ( cos θ , sin θ ) , e ^ θ = ( − sin θ , cos θ ) . Fatores de escala (Lamé): h r = 1 , h θ = r h_r=1,\ h_\theta=r h r = 1 , h θ = r
Matriz jacobiana J = ∂ ( x , y ) ∂ ( r , θ ) J=\frac{\partial(x,y)}{\partial(r,\theta)} J = ∂ ( r , θ ) ∂ ( x , y )
J = ( cos θ − r sin θ sin θ r cos θ ) , ∣ J ∣ = r . J=
\begin{pmatrix}
\cos\theta & -r\sin\theta\\
\sin\theta & \ \ r\cos\theta
\end{pmatrix},
\qquad |J|=r. J = ( cos θ sin θ − r sin θ r cos θ ) , ∣ J ∣ = r . Elemento de linha e área
d s 2 = d r 2 + r 2 d θ 2 , d A = r d r d θ . ds^2 = dr^2 + r^2\,d\theta^2,\qquad dA = r\,dr\,d\theta. d s 2 = d r 2 + r 2 d θ 2 , d A = r d r d θ . Relação com Cartesianas
x = ρ cos φ , y = ρ sin φ , z = z , ρ ≥ 0 , φ ∈ [ 0 , 2 π ) . x=\rho\cos\varphi,\quad y=\rho\sin\varphi,\quad z=z,
\qquad \rho\ge 0,\ \varphi\in[0,2\pi). x = ρ cos φ , y = ρ sin φ , z = z , ρ ≥ 0 , φ ∈ [ 0 , 2 π ) . Base ortonormal
e ^ ρ = ( cos φ , sin φ , 0 ) , e ^ φ = ( − sin φ , cos φ , 0 ) , e ^ z = ( 0 , 0 , 1 ) . \hat{\mathbf e}_\rho=(\cos\varphi,\sin\varphi,0),\quad
\hat{\mathbf e}_\varphi=(-\sin\varphi,\cos\varphi,0),\quad
\hat{\mathbf e}_z=(0,0,1). e ^ ρ = ( cos φ , sin φ , 0 ) , e ^ φ = ( − sin φ , cos φ , 0 ) , e ^ z = ( 0 , 0 , 1 ) . Fatores de escala : h ρ = 1 , h φ = ρ , h z = 1. h_\rho=1,\ h_\varphi=\rho,\ h_z=1. h ρ = 1 , h φ = ρ , h z = 1.
Matriz jacobiana
J = ( cos φ − ρ sin φ 0 sin φ ρ cos φ 0 0 0 1 ) , ∣ J ∣ = ρ . J=
\begin{pmatrix}
\cos\varphi & -\rho\sin\varphi & 0\\
\sin\varphi & \ \ \rho\cos\varphi & 0\\
0&0&1
\end{pmatrix},
\qquad |J|=\rho. J = ⎝ ⎛ cos φ sin φ 0 − ρ sin φ ρ cos φ 0 0 0 1 ⎠ ⎞ , ∣ J ∣ = ρ . Elemento de linha e volume
d s 2 = d ρ 2 + ρ 2 d φ 2 + d z 2 , d V = ρ d ρ d φ d z . ds^2=d\rho^2+\rho^2\,d\varphi^2+dz^2,\qquad
dV=\rho\,d\rho\,d\varphi\,dz. d s 2 = d ρ 2 + ρ 2 d φ 2 + d z 2 , d V = ρ d ρ d φ d z . Relação com Cartesianas (convenção: θ \theta θ φ \varphi φ
x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ , x=r\sin\theta\cos\varphi,\quad
y=r\sin\theta\sin\varphi,\quad
z=r\cos\theta, x = r sin θ cos φ , y = r sin θ sin φ , z = r cos θ , r ≥ 0 , θ ∈ [ 0 , π ] , φ ∈ [ 0 , 2 π ) . r\ge 0,\ \theta\in[0,\pi],\ \varphi\in[0,2\pi). r ≥ 0 , θ ∈ [ 0 , π ] , φ ∈ [ 0 , 2 π ) . Base ortonormal
e ^ r = ( sin θ cos φ , sin θ sin φ , cos θ ) , e ^ θ = ( cos θ cos φ , cos θ sin φ , − sin θ ) , e ^ φ = ( − sin φ , cos φ , 0 ) . \hat{\mathbf e}_r=(\sin\theta\cos\varphi,\sin\theta\sin\varphi,\cos\theta),\quad
\hat{\mathbf e}_\theta=(\cos\theta\cos\varphi,\cos\theta\sin\varphi,-\sin\theta),\quad
\hat{\mathbf e}_\varphi=(-\sin\varphi,\cos\varphi,0). e ^ r = ( sin θ cos φ , sin θ sin φ , cos θ ) , e ^ θ = ( cos θ cos φ , cos θ sin φ , − sin θ ) , e ^ φ = ( − sin φ , cos φ , 0 ) . Fatores de escala : h r = 1 , h θ = r , h φ = r sin θ . h_r=1,\ h_\theta=r,\ h_\varphi=r\sin\theta. h r = 1 , h θ = r , h φ = r sin θ .
Matriz jacobiana
J = ( sin θ cos φ r cos θ cos φ − r sin θ sin φ sin θ sin φ r cos θ sin φ r sin θ cos φ cos θ − r sin θ 0 ) , ∣ J ∣ = r 2 sin θ . J=
\begin{pmatrix}
\sin\theta\cos\varphi & r\cos\theta\cos\varphi & -r\sin\theta\sin\varphi\\
\sin\theta\sin\varphi & r\cos\theta\sin\varphi & \ \ r\sin\theta\cos\varphi\\
\cos\theta & -r\sin\theta & 0
\end{pmatrix},
\qquad |J|=r^2\sin\theta. J = ⎝ ⎛ sin θ cos φ sin θ sin φ cos θ r cos θ cos φ r cos θ sin φ − r sin θ − r sin θ sin φ r sin θ cos φ 0 ⎠ ⎞ , ∣ J ∣ = r 2 sin θ . Elemento de linha e volume
d s 2 = d r 2 + r 2 d θ 2 + r 2 sin 2 θ d φ 2 , d V = r 2 sin θ d r d θ d φ . ds^2=dr^2+r^2\,d\theta^2+r^2\sin^2\theta\,d\varphi^2,\qquad
dV=r^2\sin\theta\,dr\,d\theta\,d\varphi. d s 2 = d r 2 + r 2 d θ 2 + r 2 sin 2 θ d φ 2 , d V = r 2 sin θ d r d θ d φ . Relação com Cartesianas ( r , ϕ 1 , … , ϕ d − 1 ) (r,\phi_1,\ldots,\phi_{d-1}) ( r , ϕ 1 , … , ϕ d − 1 )
x 1 = r cos ϕ 1 , x 2 = r sin ϕ 1 cos ϕ 2 , x 3 = r sin ϕ 1 sin ϕ 2 cos ϕ 3 , ⋮ x d − 1 = r sin ϕ 1 ⋯ sin ϕ d − 2 cos ϕ d − 1 , x d = r sin ϕ 1 ⋯ sin ϕ d − 2 sin ϕ d − 1 , \begin{aligned}
x_1 &= r\cos\phi_1,\\
x_2 &= r\sin\phi_1\cos\phi_2,\\
x_3 &= r\sin\phi_1\sin\phi_2\cos\phi_3,\\
&\ \ \vdots\\
x_{d-1} &= r\sin\phi_1\cdots\sin\phi_{d-2}\cos\phi_{d-1},\\
x_d &= r\sin\phi_1\cdots\sin\phi_{d-2}\sin\phi_{d-1},
\end{aligned} x 1 x 2 x 3 x d − 1 x d = r cos ϕ 1 , = r sin ϕ 1 cos ϕ 2 , = r sin ϕ 1 sin ϕ 2 cos ϕ 3 , ⋮ = r sin ϕ 1 ⋯ sin ϕ d − 2 cos ϕ d − 1 , = r sin ϕ 1 ⋯ sin ϕ d − 2 sin ϕ d − 1 , com domínios r ≥ 0 r\ge 0 r ≥ 0 ϕ 1 , … , ϕ d − 2 ∈ [ 0 , π ] \phi_1,\ldots,\phi_{d-2}\in[0,\pi] ϕ 1 , … , ϕ d − 2 ∈ [ 0 , π ] ϕ d − 1 ∈ [ 0 , 2 π ) \phi_{d-1}\in[0,2\pi) ϕ d − 1 ∈ [ 0 , 2 π )
Base ortonormal e fatores de escala ortogonal com
h r = 1 , h ϕ k = r ∏ j = 1 k − 1 sin ϕ j ( k = 1 , … , d − 1 ) , h_r=1,\qquad
h_{\phi_k}=r\prod_{j=1}^{k-1}\sin\phi_j\quad (k=1,\ldots,d-1), h r = 1 , h ϕ k = r j = 1 ∏ k − 1 sin ϕ j ( k = 1 , … , d − 1 ) , (produto vazio = 1 =1 = 1 h ϕ 1 = r h_{\phi_1}=r h ϕ 1 = r h ϕ 2 = r sin ϕ 1 h_{\phi_2}=r\sin\phi_1 h ϕ 2 = r sin ϕ 1 e ^ q = 1 h q ∂ r / ∂ q \hat{\mathbf e}_q=\frac{1}{h_q}\,\partial \mathbf r/\partial q e ^ q = h q 1 ∂ r / ∂ q
Determinante jacobiano ∣ J ∣ = ∏ h i |J|=\prod h_i ∣ J ∣ = ∏ h i
∣ J ∣ = r d − 1 ∏ k = 1 d − 2 ( sin ϕ k ) d − 1 − k . |J|=r^{\,d-1}\,\prod_{k=1}^{d-2}\bigl(\sin\phi_k\bigr)^{\,d-1-k}. ∣ J ∣ = r d − 1 k = 1 ∏ d − 2 ( sin ϕ k ) d − 1 − k . Elemento de linha e volume
d s 2 = d r 2 + ∑ k = 1 d − 1 h ϕ k 2 d ϕ k 2 = d r 2 + r 2 [ d ϕ 1 2 + sin 2 ϕ 1 d ϕ 2 2 + ⋯ + ( ∏ j = 1 d − 2 sin 2 ϕ j ) d ϕ d − 1 2 ] , ds^2=dr^2+\sum_{k=1}^{d-1} h_{\phi_k}^2\,d\phi_k^{\,2}
=dr^2+r^2\!\left[d\phi_1^2+\sin^2\!\phi_1\,d\phi_2^2+\cdots
+\Bigl(\!\prod_{j=1}^{d-2}\sin^2\!\phi_j\Bigr)d\phi_{d-1}^2\right], d s 2 = d r 2 + k = 1 ∑ d − 1 h ϕ k 2 d ϕ k 2 = d r 2 + r 2 [ d ϕ 1 2 + sin 2 ϕ 1 d ϕ 2 2 + ⋯ + ( j = 1 ∏ d − 2 sin 2 ϕ j ) d ϕ d − 1 2 ] ,
d V = ∣ J ∣ d r d ϕ 1 ⋯ d ϕ d − 1 = r d − 1 ( ∏ k = 1 d − 2 sin d − 1 − k ϕ k ) d r d ϕ 1 ⋯ d ϕ d − 1 . dV=|J|\,dr\,d\phi_1\cdots d\phi_{d-1}
= r^{\,d-1}\!\left(\prod_{k=1}^{d-2}\sin^{\,d-1-k}\!\phi_k\right)\!dr\,d\phi_1\cdots d\phi_{d-1}. d V = ∣ J ∣ d r d ϕ 1 ⋯ d ϕ d − 1 = r d − 1 ( k = 1 ∏ d − 2 sin d − 1 − k ϕ k ) d r d ϕ 1 ⋯ d ϕ d − 1 . Uma variedade diferencial M M M n n n R n \mathbb{R}^n R n
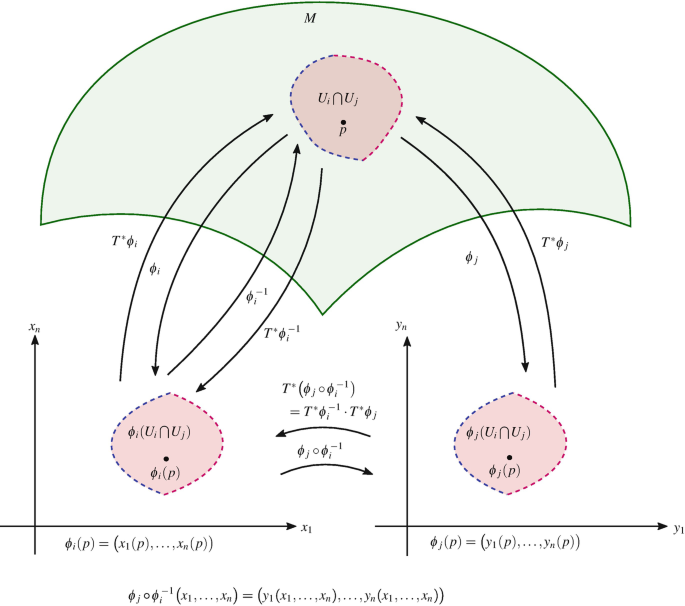
Figure 2: Uma Variedade diferencial e algumas aplicações lineares discutidas no texto abaixo.
Uma variedade diferencial n n n M \mathcal{M} M R d \mathbb{R^d} R d { U i } \{U_i\} { U i } M \mathcal{M} M { V i } \{V_i\} { V i } R d \mathbb{R^d} R d ϕ : U i ↦ V i \phi: U_i \mapsto V_i ϕ : U i ↦ V i
ϕ : U i ↦ V i \phi: U_i \mapsto V_i ϕ : U i ↦ V i U i U_i U i ϕ ( p ) \phi(p) ϕ ( p ) p p p ⋃ U i = M \bigcup U_i = \mathcal{M} ⋃ U i = M O conjunto de cartas é um atlas. Para definir vetores em uma variedade é necessário compreender que os vetores são objetos locais e não globais, formando um espaço vetorial de mesma dimensão, para cada ponto da variedade.
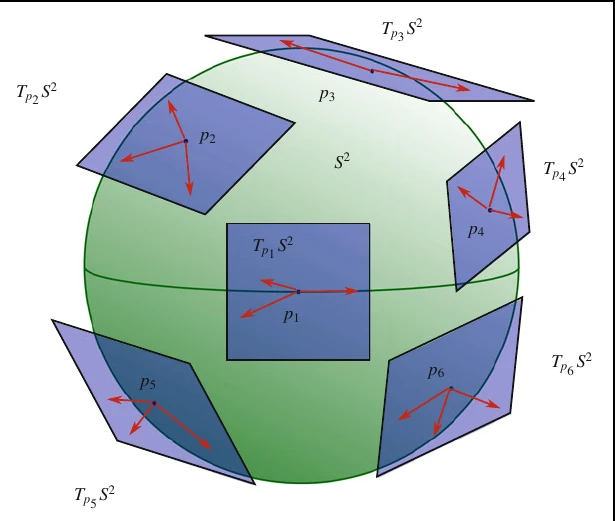
Figure 3: Visualizando os espaços tangentes da esfera S 2 S^2 S 2
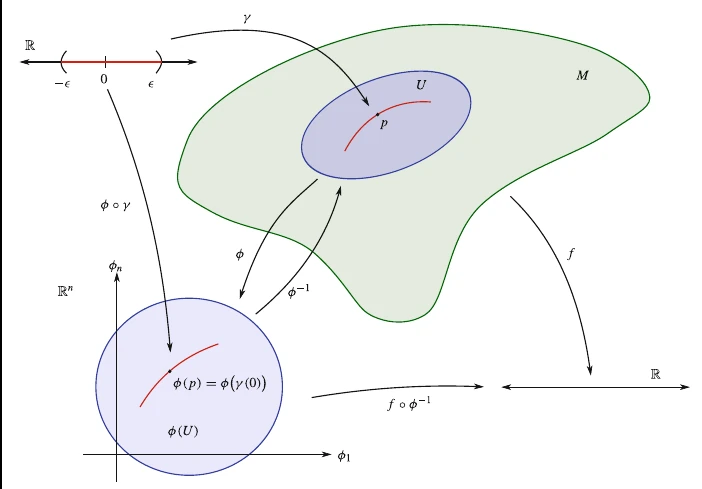
Para realizar esta construção e revelar as suas propriedades, vamos considerar um ponto p ∈ M p \in \mathcal{M} p ∈ M γ : ( − ϵ , ϵ ) ∈ R ↦ M \gamma: (-\epsilon, \epsilon) \in \mathbb{R} \mapsto \mathcal{M} γ : ( − ϵ , ϵ ) ∈ R ↦ M γ ( 0 ) = p \gamma(0) = p γ ( 0 ) = p R d \mathbb{R}^d R d p p p p p p
T p M = { [ γ ] p ∣ γ : ( − ϵ , ϵ ) ∈ R ↦ M ∧ γ ( 0 ) = p } T_pM = \left\{ [\gamma]_p \vert \gamma: (-\epsilon, \epsilon) \in \mathbb{R} \mapsto \mathcal{M} \land \gamma(0) = p \right\} T p M = { [ γ ] p ∣ γ : ( − ϵ , ϵ ) ∈ R ↦ M ∧ γ ( 0 ) = p } Figure 4: Visualizando os espaços tangentes como a derivada direcional.
Esta definição é equivalente a dizer que os vetores são operadores lineares que implementam uma diferenciação no espaço das funções suaves sobre M \mathcal{M} M X ( M ) \Chi(\mathcal{M}) X ( M )
v p [ f ] = D [ γ ] p f = ∂ ( f ∘ γ ) ∂ t ∣ t = 0 = ∂ ( f ( x i ( t ) ) ) ∂ t ∣ t = 0 = ∂ f ∂ x i ∣ γ ( 0 ) ∂ x i ∂ t ∣ t = 0 = ∂ f ∂ x i ∣ p v i \begin{aligned}
v_p[f] &= D_{[\gamma]_p} f \\
&= \left. \frac{\partial (f\circ \gamma)}{\partial t} \right \rvert_{t=0}\\
&= \left. \frac{\partial (f(x^i(t)))}{\partial t} \right \rvert_{t=0} \\
&= \left. \frac{\partial f}{\partial x^i}\right \rvert_{\gamma(0)} \left. \frac{\partial x^i}{\partial t} \right \rvert_{t=0} \\
&= \left. \frac{\partial f}{\partial x^i}\right \rvert_{p} v^i
\end{aligned} v p [ f ] = D [ γ ] p f = ∂ t ∂ ( f ∘ γ ) ∣ ∣ t = 0 = ∂ t ∂ ( f ( x i ( t ))) ∣ ∣ t = 0 = ∂ x i ∂ f ∣ ∣ γ ( 0 ) ∂ t ∂ x i ∣ ∣ t = 0 = ∂ x i ∂ f ∣ ∣ p v i O espaço tangente T p M T_pM T p M p ∈ M p\in M p ∈ M M M M p p p
Em coordenadas locais ( x 1 , … , x n ) (x^1,\dots,x^n) ( x 1 , … , x n ) T p M T_pM T p M
{ ∂ ∂ x 1 ∣ p , … , ∂ ∂ x n ∣ p } . \left\{ \frac{\partial}{\partial x^1}\Big|_p, \dots, \frac{\partial}{\partial x^n}\Big|_p \right\}. { ∂ x 1 ∂ ∣ ∣ p , … , ∂ x n ∂ ∣ ∣ p } . O espaço cotangente T p ∗ M T_p^*M T p ∗ M T p M T_pM T p M
A base dual é dada por { d x 1 ∣ p , … , d x n ∣ p } \{dx^1|_p, \dots, dx^n|_p\} { d x 1 ∣ p , … , d x n ∣ p } d x i ( ∂ ∂ x j ) = δ j i dx^i\!\left(\tfrac{\partial}{\partial x^j}\right)=\delta^i_j d x i ( ∂ x j ∂ ) = δ j i
Seja L L L L ⋆ L^\star L ⋆ ( p , q ) (p, q) ( p , q )
t : L × L ⋯ × L × L ⋆ ⏟ q × L ⋆ ⋯ × L ⋆ ⏟ p ↦ R ( v i 1 , … v i q ; ω j 1 , … ω j p ) ↦ t ( v i 1 , … v i q ; ω j 1 , … ω j p ) ∈ R t ( … v i q + λ w … ) = t ( … v i q … ) + + λ t ( … w … ) t: \underbrace{L \times L \cdots \times L \times L^\star}_{q} \underbrace{\times L^\star \cdots \times L^\star}_{p} \mapsto \mathbb{R} \\
(v_{i_1}, \ldots v_{i_q}; \omega_{j_1}, \ldots \omega_{j_p}) \mapsto t(v_{i_1}, \ldots v_{i_q}; \omega_{j_1}, \ldots \omega_{j_p}) \in \mathbb{R}\\
t(\ldots v_{i_q} + \lambda w \ldots) = t(\ldots v_{i_q} \ldots) + + \lambda t(\ldots w \ldots) t : q L × L ⋯ × L × L ⋆ p × L ⋆ ⋯ × L ⋆ ↦ R ( v i 1 , … v i q ; ω j 1 , … ω j p ) ↦ t ( v i 1 , … v i q ; ω j 1 , … ω j p ) ∈ R t ( … v i q + λ w … ) = t ( … v i q … ) + + λ t ( … w … ) para todas as posições. O espaço vetorial obtido com a coleção destes objetos é o espaço T q p ( L ) T_q^p(L) T q p ( L ) T 0 0 ( L ) ≡ R T_0^0(L) \equiv \mathbb{R} T 0 0 ( L ) ≡ R
Dado o espaço dos tensores T p 0 ( L ) T_p^0(L) T p 0 ( L ) ω \omega ω Ω p \Omega^p Ω p
Ω 0 ≡ R \Omega^0 \equiv \mathbb{R} Ω 0 ≡ R Ω 1 ≡ T 1 0 ( M ) ≡ T p ⋆ ( M ) \Omega^1 \equiv T_1^0(\mathbb{M}) \equiv T_p^\star(M) Ω 1 ≡ T 1 0 ( M ) ≡ T p ⋆ ( M ) Podemos definir uma operação de projeção:
π A : T p 0 ↦ Ω p ( π A t ) ( v i 1 , … , v i p ) = 1 p ! ∑ σ t ( σ ( v i 1 , … , v i p ) ) \pi^A: T_p^0 \mapsto \Omega^p \\
(\pi^A t)(v_{i_1},\ldots,v_{i_p}) = \frac{1}{p!}\sum_\sigma t(\sigma(v_{i_1},\ldots,v_{i_p})) π A : T p 0 ↦ Ω p ( π A t ) ( v i 1 , … , v i p ) = p ! 1 σ ∑ t ( σ ( v i 1 , … , v i p )) E agora podemos definir uma estrutura algébrica utilizando o produto exterior:
∧ : Ω p × Ω q ↦ Ω p + q ( α , ∧ ) ↦ α ∧ β α ∧ β ≡ ( p + q ) ! p ! q ! π A ( α ⊗ β ) \wedge : \Omega^p \times \Omega^q \mapsto \Omega^{p+q} \\
(\alpha, \wedge) \mapsto \alpha \wedge \beta \\
\alpha \wedge \beta \equiv \frac{(p+q)!}{p!q!}\pi^A(\alpha \otimes \beta) ∧ : Ω p × Ω q ↦ Ω p + q ( α , ∧ ) ↦ α ∧ β α ∧ β ≡ p ! q ! ( p + q )! π A ( α ⊗ β ) e pode-se mostrar sem dificuldade que este produto é bilinear , associativo e m a t h b b Z mathbb{Z} ma t hbb Z
α ∧ β = ( − 1 ) p q β α . \alpha \wedge \beta = (-1)^{pq} \beta \alpha. α ∧ β = ( − 1 ) pq β α . Em coordenadas, uma 1-forma é
α = α i ( x ) d x i , \alpha = \alpha_i(x)\,dx^i, α = α i ( x ) d x i , e uma 2-forma é
β = 1 2 β i j ( x ) d x i ∧ d x j , β i j = − β j i . \beta = \tfrac{1}{2}\beta_{ij}(x)\,dx^i\wedge dx^j,\quad \beta_{ij}=-\beta_{ji}. β = 2 1 β ij ( x ) d x i ∧ d x j , β ij = − β ji . Em uma variedade n n n p p p Ω p ( M ) \Omega^p(M) Ω p ( M )
dim Ω p ( M ) = ( n p ) . \dim \Omega^p(M)=\binom{n}{p}. dim Ω p ( M ) = ( p n ) . A derivada exterior d : Ω k ( M ) → Ω k + 1 ( M ) d:\Omega^k(M)\to\Omega^{k+1}(M) d : Ω k ( M ) → Ω k + 1 ( M )
d ( f ) = d f = ∂ i f d x i d(f)=df=\partial_i f\, dx^i d ( f ) = df = ∂ i f d x i satisfaz linearidade, regra de Leibniz e d 2 = 0 d^2=0 d 2 = 0 Exemplo em R 3 \mathbb{R}^3 R 3 α = f d x + g d y + h d z \alpha = f\,dx+g\,dy+h\,dz α = f d x + g d y + h d z
d α = ( ∂ x g − ∂ y f ) d x ∧ d y + ( ∂ y h − ∂ z g ) d y ∧ d z + ( ∂ z f − ∂ x h ) d z ∧ d x . d\alpha = (\partial_x g - \partial_y f)\,dx\wedge dy + (\partial_y h - \partial_z g)\,dy\wedge dz + (\partial_z f - \partial_x h)\,dz\wedge dx. d α = ( ∂ x g − ∂ y f ) d x ∧ d y + ( ∂ y h − ∂ z g ) d y ∧ d z + ( ∂ z f − ∂ x h ) d z ∧ d x . Aplicações de tensores e campos ¶ Dadas duas variedades M , N \mathcal{M}, \mathcal{N} M , N χ , ψ , f \chi, \psi, f χ , ψ , f
R ← χ M → f N → ψ R , \mathbb{R} \xleftarrow{\chi} \mathcal{M} \xrightarrow{f} \mathcal{N} \xrightarrow{\psi} \mathbb{R}, R χ M f N ψ R , Vemos que a aplicação ψ \psi ψ
M → f N → ψ R ψ ∘ f : M → R , \mathcal{M} \xrightarrow{f} \mathcal{N} \xrightarrow{\psi} \mathbb{R} \\
\psi \circ f: \mathcal{M} \rightarrow \mathbb{R}, M f N ψ R ψ ∘ f : M → R , contudo a operação semelhante com a função χ \chi χ f f f pulled back .
Funções são campos tensoriais de tipo ( 0 , 0 ) (0,0) ( 0 , 0 )
Seja f : M → N f: \mathcal{M} \rightarrow \mathcal{N} f : M → N ψ : N → R \psi : \mathcal{N} \rightarrow \mathbb{R} ψ : N → R N \mathcal{N} N
f ⋆ ψ : = ψ ∘ f f^\star \psi := \psi \circ f f ⋆ ψ := ψ ∘ f f ⋆ : M → R f^\star: \mathcal{M} \rightarrow \mathbb{R} f ⋆ : M → R Em coordenadas locais:
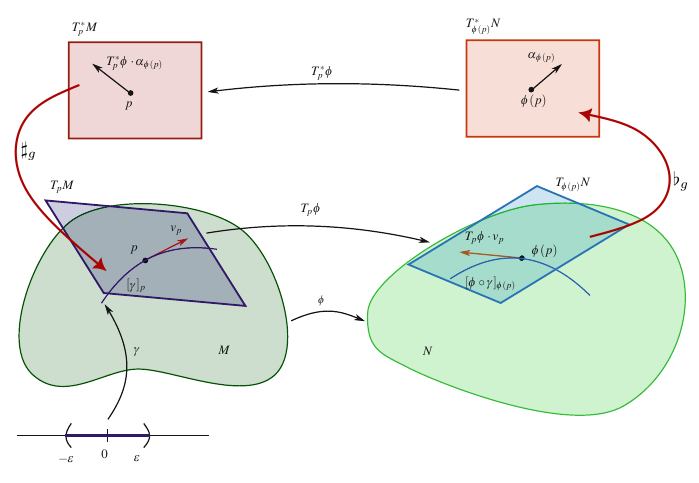
f : x i ↦ y i ⇒ ( f ⋆ ψ ) ( x ) = ψ ( y ( x ) ) f: x^i \mapsto y^i \Rightarrow (f^\star \psi)(x) = \psi(y(x)) f : x i ↦ y i ⇒ ( f ⋆ ψ ) ( x ) = ψ ( y ( x )) Para uma composição M → f N → g S \mathcal{M} \xrightarrow{f} \mathcal{N} \xrightarrow{g} \mathcal{S} M f N g S ( g ∘ f ) ⋆ = f ⋆ ∘ g ⋆ (g\circ f)^\star = f^\star\circ g^\star ( g ∘ f ) ⋆ = f ⋆ ∘ g ⋆ A aplicação tangente, ou o diferencial, ou ainda o pushforward é
T x f ≡ f ⋆ : T x M → T f ( x ) N f ⋆ [ γ ] ≡ [ f ∘ γ ] f ⋆ ( V i ∂ i ) = ( ∂ y a ∂ x i V i ) ∂ a T_x f \equiv f_\star: T_x\mathcal{M} \rightarrow T_{f(x)} \mathcal{N}\\
f_\star[\gamma] \equiv [f\circ \gamma]\\
f_\star(V_i\partial_i) = (\frac{\partial y^a}{\partial x^i} V^i) \partial_a T x f ≡ f ⋆ : T x M → T f ( x ) N f ⋆ [ γ ] ≡ [ f ∘ γ ] f ⋆ ( V i ∂ i ) = ( ∂ x i ∂ y a V i ) ∂ a Em coordenadas locais:
f : x i ↦ y i ⇒ ( f ⋆ ψ ) ( x ) = ψ ( y ( x ) ) f: x^i \mapsto y^i \Rightarrow (f^\star \psi)(x) = \psi(y(x)) f : x i ↦ y i ⇒ ( f ⋆ ψ ) ( x ) = ψ ( y ( x )) Para uma composição M → f N → g S \mathcal{M} \xrightarrow{f} \mathcal{N} \xrightarrow{g} \mathcal{S} M f N g S ( g ∘ f ) ⋆ = f ⋆ ∘ g ⋆ (g\circ f)^\star = f^\star\circ g^\star ( g ∘ f ) ⋆ = f ⋆ ∘ g ⋆ Aplicando isto para o espaço dos covetores:
f : N ↦ N f ⋆ : T f ( x ) ⋆ N → T f ( x ) ⋆ M ⟨ f ⋆ α , V ⟩ ≡ ⟨ α , f ⋆ V ⟩ f ⋆ d y a = ∂ y a ∂ x i d x i = J i a d x i f: \mathcal{N} \mapsto \mathcal{N}\\
f^\star: T^\star_{f(x)}\mathcal{N} \rightarrow T^\star_{f(x)}\mathcal{M}
\langle f\star \alpha, V\rangle \equiv \langle \alpha, f_\star V\rangle \\
f^\star dy^a = \frac{\partial y^a}{\partial x^i} dx^i = J^a_i dx^i f : N ↦ N f ⋆ : T f ( x ) ⋆ N → T f ( x ) ⋆ M ⟨ f ⋆ α , V ⟩ ≡ ⟨ α , f ⋆ V ⟩ f ⋆ d y a = ∂ x i ∂ y a d x i = J i a d x i covetores e campos covariantes podem ser propagados usando o pullback , definindo campos em variedades derivadas. O procedimento não se generaliza para campos vetoriais. Apenas de f f f difeomorfismo podemos propagar os campos vetoriais via puhforward .
Métrica ¶ Em uma variedade M \mathcal{M} M ( p , q ) (p, q) ( p , q )
1 ^ ⟨ V , α ⟩ ⟨ α , V ⟩ ⇒ 1 ^ ⟨ V , ⋅ ⟩ = V , 1 ^ ⟨ ⋅ , α ⟩ = α 1 ^ = d x i ⊗ ∂ j ⇒ 1 ^ j 1 = δ j i \hat{\mathbb{1}} \langle V, \alpha \rangle
\langle \alpha, V \rangle \Rightarrow \hat{\mathbb{1}} \langle V, \cdot \rangle = V, \hat{\mathbb{1}} \langle \cdot, \alpha \rangle = \alpha \\
\hat{\mathbb{1}} = dx^i\otimes \partial_j \Rightarrow \hat{\mathbb{1}}^1_j = \delta^i_ j 1 ^ ⟨ V , α ⟩ ⟨ α , V ⟩ ⇒ 1 ^ ⟨ V , ⋅ ⟩ = V , 1 ^ ⟨ ⋅ , α ⟩ = α 1 ^ = d x i ⊗ ∂ j ⇒ 1 ^ j 1 = δ j i Um tensor ( 0 , 2 ) (0,2) ( 0 , 2 )
Produto interno de vetores Elemento de Linha Isomorfismos musicais Abaixamento e levantamento de índices (via isomorfismos musicais) Forma de volume (acrescida de uma orientação) g ∈ T 2 0 ⇒ g : T p M × T p M ↦ R g ( U , V ) = g ( V , U ) ∧ g ( U , U ) ≥ 0 ∧ g ( U , U ) = 0 ⇔ U ≡ 0 g ( U , V ) = ( g i j d x i ⊗ d x j ) ( U k ∂ k , V l ∂ l ) = g i j U k V l ( d x i ⊗ ∂ k ) ( d x i ⊗ ∂ k ) = g i j U k V l δ k i δ l j = g i j U i V j ♭ g : T p M ↦ T p ⋆ M ♭ g ( V i ∂ i ) = g i j V j d x i = V i d x i ♯ g : T p ⋆ M ↦ T p M ♯ g ( ω i d x i ) = g i j ω i ∂ i = ω i ∂ i g i j ( x ) = ⟨ ∂ i , ∂ j ⟩ = ⟨ ∂ x ′ r ∂ x i ∂ r ′ , ∂ x ′ s ∂ x j ∂ s ′ ⟩ ⇒ g i j = ∂ x ′ r ∂ x i ∂ x ′ r ∂ x i g r s ′ d s 2 = g i j d x i d x j \begin{aligned}
g \in \mathcal{T}^0_2 &\Rightarrow g: T_p\mathcal{M} \times T_p\mathcal{M} \mapsto \mathbb{R}\\
g(U, V) = g(V, U) \;&\land g(U, U) \ge 0 \; \land g(U, U)=0 \Leftrightarrow U \equiv 0 \\
g(U, V) &= (g_{ij} dx^i\otimes dx^j )(U^k\partial_k, V^l\partial_l) \\
&= g_{ij} U^k V^l (dx^i \otimes \partial_k) (dx^i \otimes \partial_k) \\
&= g_{ij} U^k V^l \delta^i_k \delta^j_l = g_{ij} U^i V^j\\
\flat_g: T_p\mathcal{M} &\mapsto T^\star_p\mathcal{M}\\
\flat_g (V^i\partial_i) &= g_{ij} V^j dx^i = V_i dx^i \\
\sharp_g: T^\star_p\mathcal{M} &\mapsto T_p\mathcal{M}\\
\sharp_g (\omega_i dx^i) &= g^{ij} \omega_i \partial_i = \omega^i \partial_i \\
g_{ij}(x) &= \langle \partial_i, \partial_j \rangle \\
&= \langle \frac{\partial x'^r}{\partial x^i} \partial'_r, \frac{\partial x'^s}{\partial x^j}\partial'_s\rangle \Rightarrow\\
g_{ij} &= \frac{\partial x'^r}{\partial x^i}\frac{\partial x'^r}{\partial x^i} g'_{rs} \\
ds^2 &= g_{ij} dx^i dx^j
\end{aligned} g ∈ T 2 0 g ( U , V ) = g ( V , U ) g ( U , V ) ♭ g : T p M ♭ g ( V i ∂ i ) ♯ g : T p ⋆ M ♯ g ( ω i d x i ) g ij ( x ) g ij d s 2 ⇒ g : T p M × T p M ↦ R ∧ g ( U , U ) ≥ 0 ∧ g ( U , U ) = 0 ⇔ U ≡ 0 = ( g ij d x i ⊗ d x j ) ( U k ∂ k , V l ∂ l ) = g ij U k V l ( d x i ⊗ ∂ k ) ( d x i ⊗ ∂ k ) = g ij U k V l δ k i δ l j = g ij U i V j ↦ T p ⋆ M = g ij V j d x i = V i d x i ↦ T p M = g ij ω i ∂ i = ω i ∂ i = ⟨ ∂ i , ∂ j ⟩ = ⟨ ∂ x i ∂ x ′ r ∂ r ′ , ∂ x j ∂ x ′ s ∂ s ′ ⟩ ⇒ = ∂ x i ∂ x ′ r ∂ x i ∂ x ′ r g rs ′ = g ij d x i d x j Figure 5: Visualizando os espaços tangentes, cotangente, pullback, pushforward e isomorfismos musicais.
Em uma variedade orientada com métrica g g g forma de volume é
v o l = ∣ g ∣ d x 1 ∧ ⋯ ∧ d x n , \mathrm{vol} = \sqrt{|g|}\, dx^1\wedge\cdots\wedge dx^n, vol = ∣ g ∣ d x 1 ∧ ⋯ ∧ d x n , onde ∣ g ∣ = det ( g i j ) |g|=\det(g_{ij}) ∣ g ∣ = det ( g ij )
Seja um espaço linear n-dimensional L L L g g g o o o ω ≡ ω g , o \omega \equiv \omega_{g,o} ω ≡ ω g , o
α ↦ ⋆ α , α ∈ Ω p L , ⋆ α ∈ Ω n − p L ⋆ α i 1 … i p : = 1 p ! α i p + 1 … i n ω i 1 … i p i p + 1 … i n ⋆ g 1 = ω g ⋆ ω g = s i g n g ⋆ g ⋆ g = s i g n g ( − 1 ) p ( n − p ) α ∧ ⋆ g β = ⟨ α , β ⟩ g ω g \alpha \mapsto \star\alpha, \quad \alpha \in \Omega^pL, \quad \star \alpha \in \Omega^{n-p}L \\
\star \alpha_{i_1\ldots i_p} := \frac{1}{p!}\alpha^{i_{p+1}\ldots i_{n}}\omega_{i_1\ldots i_p\;i_{p+1}\ldots i_{n}}\\
\star_g \mathbb{1} = \omega_g \\
\star \omega_g = \mathrm{sign}\;g \\
\star_g \star_g = \mathrm{sign}\;g (-1)^{p(n-p)}\\
\alpha \wedge \star_g \beta = \langle \alpha, \beta \rangle_g\; \omega_g α ↦ ⋆ α , α ∈ Ω p L , ⋆ α ∈ Ω n − p L ⋆ α i 1 … i p := p ! 1 α i p + 1 … i n ω i 1 … i p i p + 1 … i n ⋆ g 1 = ω g ⋆ ω g = sign g ⋆ g ⋆ g = sign g ( − 1 ) p ( n − p ) α ∧ ⋆ g β = ⟨ α , β ⟩ g ω g A coderivada δ : Ω k ( M ) → Ω k − 1 ( M ) \delta:\Omega^k(M)\to\Omega^{k-1}(M) δ : Ω k ( M ) → Ω k − 1 ( M )
δ = ( − 1 ) n ( k + 1 ) + 1 d . \delta = (-1)^{n(k+1)+1} d. δ = ( − 1 ) n ( k + 1 ) + 1 d . Ela é o adjunto formal da derivada exterior em relação ao produto interno definido pela métrica.
O Laplaciano de Hodge é
Δ = d δ + δ d . \Delta = d\delta+\delta d. Δ = d δ + δ d . Em funções escalares (0-formas), em R n \mathbb{R}^n R n
Δ f = ∑ i = 1 n ∂ i 2 f . \Delta f = \sum_{i=1}^n \partial_i^2 f. Δ f = i = 1 ∑ n ∂ i 2 f . Os operadores diferenciais usuais em 3 dimensões podem ser definidos de forma simples com este formalismo:
Gradiente :
f ∈ X ( M ) ≅ Ω 0 → d d f ∈ Ω 1 → # ∇ f ∈ T p M . ∇ : X ( M ) ↦ T p M ∇ f = ( d f ) ♯ = ∑ i 1 h i ∂ f ∂ u i e ^ i . \begin{aligned}
f \in \Chi(\mathcal{M}) \cong \Omega^0 &\xrightarrow{\,d\,} df \in \Omega^1 \xrightarrow{\,\#\,} \nabla f \in T_p\mathcal{M}. \\
\nabla: \Chi(\mathcal{M}) &\mapsto T_p\mathcal{M} \\
\nabla f &= (df)^\sharp \\
&=\sum_i \frac{1}{h_i}\frac{\partial f}{\partial u^i}\, \hat e_i.
\end{aligned} f ∈ X ( M ) ≅ Ω 0 ∇ : X ( M ) ∇ f d df ∈ Ω 1 # ∇ f ∈ T p M . ↦ T p M = ( df ) ♯ = i ∑ h i 1 ∂ u i ∂ f e ^ i . Divergente :
A ( vetor ) → b A b ( 1-forma ) → ⋆ ( 2-forma ) → d ( 3-forma ) → ⋆ ( 0-forma ) \mathbf{A}\;(\text{vetor}) \xrightarrow{\,b\,} \mathbf{A}^b\;(\text{1-forma})
\xrightarrow{\,\star\,} (\text{2-forma})
\xrightarrow{\,d\,} (\text{3-forma})
\xrightarrow{\,\star\,} (\text{0-forma}) A ( vetor ) b A b ( 1-forma ) ⋆ ( 2-forma ) d ( 3-forma ) ⋆ ( 0-forma ) ∇ ⋅ X = ∗ d ( X ♭ ) = 1 h 1 h 2 h 3 ∑ i ∂ ∂ u i ( h 1 h 2 h 3 h i X i ) . = 1 ∣ g ∣ ∂ i ( ∣ g ∣ A i ) , \nabla \cdot X = * d (X^\flat) = \frac{1}{h_1 h_2 h_3}
\sum_i \frac{\partial}{\partial u^i}\Bigg(
\frac{h_1 h_2 h_3}{h_i} X^i
\Bigg). = \frac{1}{\sqrt{|g|}} \partial_i\!\bigl(\sqrt{|g|}\, A^i\bigr), ∇ ⋅ X = ∗ d ( X ♭ ) = h 1 h 2 h 3 1 i ∑ ∂ u i ∂ ( h i h 1 h 2 h 3 X i ) . = ∣ g ∣ 1 ∂ i ( ∣ g ∣ A i ) , Rotacional :
A ( vetor ) → b A b ( 1-forma ) → d ( 2-forma ) → ∗ ( 1-forma ) → # ( vetor ) = ∇ × A . \mathbf{A}\;(\text{vetor}) \xrightarrow{\,b\,} \mathbf{A}^b\;(\text{1-forma})
\xrightarrow{\,d\,} (\text{2-forma})
\xrightarrow{\,*\,} (\text{1-forma})
\xrightarrow{\,\#\,} (\text{vetor}) = \nabla\times\mathbf{A}. A ( vetor ) b A b ( 1-forma ) d ( 2-forma ) ∗ ( 1-forma ) # ( vetor ) = ∇ × A .
∇ × X = ( ∗ d X ♭ ) ♯ = 1 h j h k [ ∂ ∂ u j ( h k X k ) − ∂ ∂ u k ( h j X j ) ] = 1 ∣ g ∣ ε i j k ∂ j ( g k ℓ A ℓ ) , \nabla \times X = (* d X^\flat)^\sharp = \frac{1}{h_j h_k}
\left[
\frac{\partial}{\partial u^j}(h_k X^k) -
\frac{\partial}{\partial u^k}(h_j X^j)
\right] = \frac{1}{\sqrt{|g|}} \varepsilon^{ijk} \partial_j (g_{k\ell} A^\ell), ∇ × X = ( ∗ d X ♭ ) ♯ = h j h k 1 [ ∂ u j ∂ ( h k X k ) − ∂ u k ∂ ( h j X j ) ] = ∣ g ∣ 1 ε ijk ∂ j ( g k ℓ A ℓ ) , Laplaciano :
Δ f = δ d f = − d d f = 1 h 1 h 2 h 3 ∑ i ∂ ∂ u i ( h 1 h 2 h 3 h i 2 ∂ f ∂ u i ) = 1 ∣ g ∣ ∂ i ( ∣ g ∣ g i j ∂ j f ) . \Delta f = \delta d f = - d df = \frac{1}{h_1 h_2 h_3}
\sum_i \frac{\partial}{\partial u^i}
\Bigg( \frac{h_1 h_2 h_3}{h_i^2} \frac{\partial f}{\partial u^i} \Bigg) = \frac{1}{\sqrt{|g|}} \partial_i\!\Bigl(\sqrt{|g|}\, g^{ij}\partial_j f\Bigr). Δ f = δ df = − ddf = h 1 h 2 h 3 1 i ∑ ∂ u i ∂ ( h i 2 h 1 h 2 h 3 ∂ u i ∂ f ) = ∣ g ∣ 1 ∂ i ( ∣ g ∣ g ij ∂ j f ) . Vamos utilizar este poderoso formalismo para revelar a estrutura íntima das equações de Maxwell.