Introdução¶
Embora parece evidente, para nós, que a Terra é redonda, que orbita em torno do Sol, que as distâncias entre os astros é verdadeiramente imensa e que o Sol é muito maior do que a Terra, estes fatos tem pouco de evidente e nós simplesmente aprendemos desde cedo os resultados de muitos séculos de ciência.
Estudar como a civilização conseguiu medir estas grandezas é um exercício que permite compreender a quantidade de sutilezas existentes nas observações que fazemos de coisas eternamente em movimento, em sistemas não inerciais, fora da zona de conforto dos cursos de Física Básica.
Nesta unidade vamos reproduzir as experiências de Eratóstenes, que determinou o raio da Terra, e de Aristarco, que tentou determinar as distâncias entre a Terra e a Lua e a Terra e o Sol.
Para reproduzir estes resultados vamos utilizar um código em Python e várias visualizações. Embora estejamos fazendo uma simulação, vamos tentar, a medida do possível, obter do código as grandezas que os idealizador dos experimentos poderiam obter com medições disponíveis à época.
Não há dificuldade técnica significativa no código, mas há muitos conceitos de Astronomia ali. É muito instrutivo que o leitor procure acompanhar o que o código faz.
O experimento de Eratóstenes¶
200 anos antes da era comum, o egípcio-grego Eratóstenes criou um método simples e engenhoso para determinar o raio da Terra. Foram necessárias algumas aproximações e uma certa dose de sorte para estar no lugar certo para fazer a medida.
Vamos simular esta medida e assim não vamos precisar contar os nossos passos em uma viagem de mais de 800 km, porque para isso utilizaremos um modelo geodésico.
Embora a experiência pareça bem simples, existe uma riqueza de sutilezas que devem ser consideradas, e muito o que aprender.
Ele sabia que, no solstício de Verão, havia um poço na cidade de Aswan (na denominação moderna) que refletia o Sol ao meio-dia, portanto a sombra dos objetos verticais tinha comprimento zero e este raio de Sol deveria passar, no seu prolongamento, pelo centro da Terra.
Com uma geometria simples, medindo o tamanho da sombra em outro lugar, seria possível determinar o raio da Terra. A medida do tamanho da sombra foi realizada em Alexandria.
Uma imagem pode esclarecer a ideia.
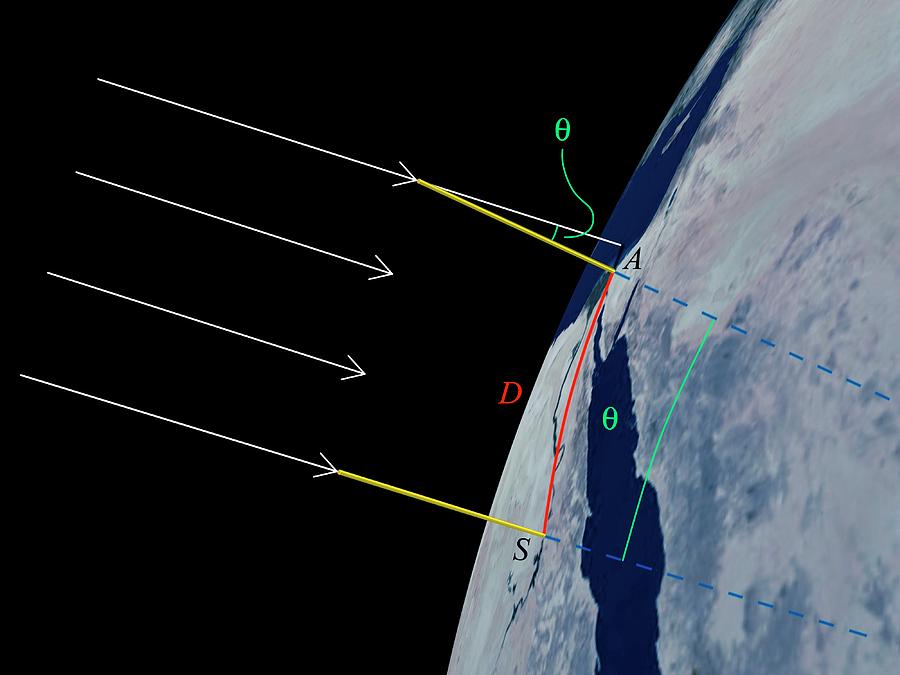
Uma ideia sensacional. Créditos da figura [1]
Vamos então seguir o seguinte roteiro:
- Vamos obter as coordenadas geográficas das cidades de Alexandria e Aswan.
- Vamos usar a biblioteca
osmnxpara obter os objetosgeocodecomo coordenadas Lat e Lon.
- Vamos usar a biblioteca
- Utilizando
geopypodemos obter a distância geodésica entre as duas cidades de maneira bastante direta. - Vamos escolher o ano para nosso experimento, uma época em que o idealizador estava vivo.
- Precisamos determinar o dia do solstício de verão.
- Vamos utilizar a biblioteca
skyfieldpara realizar os cálculos astronômicos. - Precisamos de informações sobre as posições do Sol e da Terra neste ano.
- O serviço de efemérides JPL/NASA pode fornecer os dados que queremos.
- Vamos utilizar a biblioteca
- Precisamos determinar o meio-dia local nas duas cidades.
- Já temos como calcular a posição do Sol, vamos determinar as passagens do Sol pelo meridiano local.
- A partir do meio-dia em Aswan, vamos contruir um vetor de tempos com duração de duas horas e examinar o tamanho da sombra projetada pelo Sol nas duas cidades.
- Vamos fazer uma visualização em 3D para ver como seria a sombra no chão.
- Vamos fazer um gráfico com o tamanho das sombras.
- Vamos obter uma estimativa do radio da Terra fazendo a mesma suposição de eratóstenes.
- Vamos agora fazer um raciocínio inverso e usar nossos dados para obter a latitude e longitude e a partir destas informações calcular o Raio da Terra levando em conta as posições reais das cidades, que poderiam ser medidas na época antiga se houvessem relógios confiáveis.