Source
import pyvista as pv
from src.astroufcg.grecia.eratostenes import (
set_experiment,
view_shadow_length,
view_shadow_3D,
setup
)
path = "../../../"
setup(path)
pv.set_jupyter_backend('trame')Setup¶
A função set_experimento é responsável por:
- Determinar o solstício de verão.
- Determinar a passagem do Sol no meridiano das duas cidades.
- Calcular as coordenadas horizontais (Alt, Az) para o Sol em cada uma das cidades em um intervalo de 2 horas centrado no meio-dia.
- Calcular a comprimento da sombra nos dois locais.
- Retorna um
pandas.DataFrame.
# Escolhendo os locais e o ano do experimento
alexandria = "alexandria, egypt"
aswan = "aswan, egypt"
df = set_experiment(alexandria, aswan, year=-200, object_height=10)Visualização da Sombra em 3D¶
from IPython.display import SVG
SVG("../../00_images/cap_01/alexandria_shadow.svg")Loading...
O comprimento da sombra como função do tempo¶
Source
view_shadow_length(df)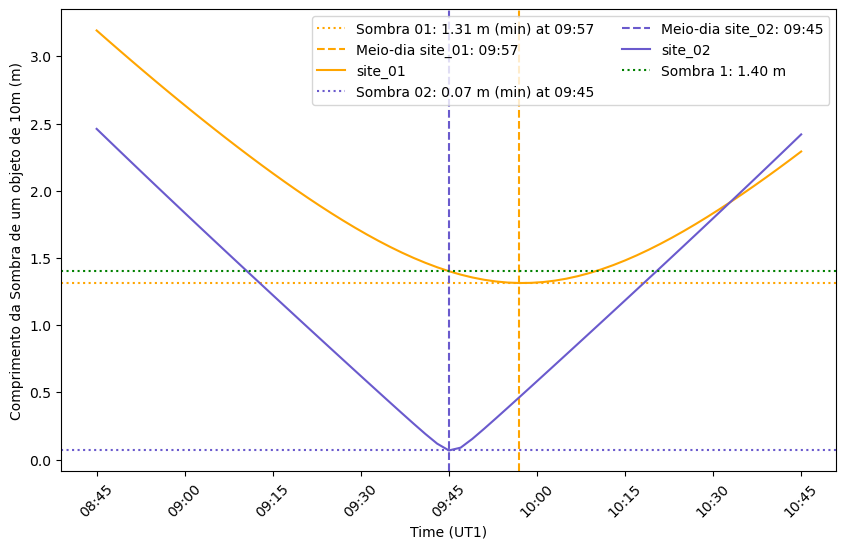
Source
from geopy.distance import geodesic, great_circle
import osmnx as ox
import numpy as np
from rich.console import Console
from rich.table import Table
h = 10
alexandria_coords = ox.geocode(alexandria)
aswan_coords = ox.geocode(aswan)
distance = geodesic(alexandria_coords, aswan_coords).km
great_circle_distance = great_circle(alexandria_coords, aswan_coords).km
noon_aswan = df["time_02"].iloc[df.reset_index()["shadow_length_02"].idxmin()]
noon_alexandria = df["time_02"].iloc[df.reset_index()["shadow_length_01"].idxmin()]
shadow_length_01 = df[df.time_02==noon_aswan]["shadow_length_01"].values[0]
shadow_length_02 = df[df.time_02==noon_aswan]["shadow_length_02"].values[0]
min_shadow_01 = df[df.time_02==noon_alexandria]["shadow_length_01"].values[0]
sol_coords_01 = df[df.time_02==noon_aswan][["alt_01", "az_01"]].values[0]
sol_coords_02 = df[df.time_02==noon_aswan][["alt_02", "az_02"]].values[0]
sol_coords_a = df[df.time_02==noon_alexandria][["alt_01", "az_01"]].values[0]
theta_alexandria = np.arctan(shadow_length_01 / h) # Assuming object height is 10
theta_aswan = np.arctan(shadow_length_02 / h) # Assuming object height is 10
R_terra = distance / theta_alexandria
Reproduzindo o Experimento de Eratosthenes¶
Source
table = Table(title="Experimento de Erathostenes")
table.add_column("Grandezas", justify="right", style="cyan", no_wrap=True)
table.add_column("Alexandria", style="yellow")
table.add_column("Aswann", justify="right", style="green")
table.add_row("meio-dia", noon_alexandria.strftime("%H:%M"), noon_aswan.strftime("%H:%M"))
table.add_row("coordenadas", f"{alexandria_coords[0]:.2f}, {alexandria_coords[1]:.2f}", f"{aswan_coords[0]:.2f}, {aswan_coords[1]:.2f}")
table.add_row("sombra", f"{shadow_length_01:.2f} m", f"{shadow_length_02:.2f} m")
table.add_row("ângulo", f"{np.degrees(theta_alexandria):.2f}°", f"{np.degrees(theta_aswan):.2f}°")
table.add_row("Sol meio-dia", f"alt: {sol_coords_a[0]:.2f}°, az: {sol_coords_a[1]:.2f}°", f"alt: {sol_coords_02[0]:.2f}°, az: {sol_coords_02[1]:.2f}°")
table.add_row("Sol meio-dia aswan", f"alt: {sol_coords_01[0]:.2f}°, az: {sol_coords_01[1]:.2f}°", f"alt: {sol_coords_02[0]:.2f}°, az: {sol_coords_02[1]:.2f}°")
d_theta = np.degrees(theta_aswan - theta_alexandria)
d_phi = np.abs((noon_alexandria - noon_aswan).total_seconds()) * 24 / 3600 # Convertendo de segundos para horas
console = Console()
console.print(table)
Loading...
Aprendendo sobre Latitudes e Longitudes¶
A diferença de Latitude é a diferença de altura do Sol nos dois locais, medidos na mesma hora.
# O sinal é porque a altitude do sol é 90 menos o angulo da sombra
delta_lat = float(-(sol_coords_a - sol_coords_02)[0])
console.print(f"Delta latitude: {delta_lat:.2f}°")Loading...
A diferença de longitude é a diferença de tempo para as passagens no meridiano, convertida em horas. Falta apenas calcular o tempo em Alexandria.
# O sinal esta relacionado com a rotação da terra
delta_t = (noon_alexandria - noon_aswan).total_seconds()
# Convertendo em graus
delta_lon = float(-delta_t * 360 / (24 * 3600)) # 24 hours in seconds
console.print(f"Delta longitude: {delta_lon:.2f}°")Loading...
Comparando com os dados geográficos temos:
def format_list(lst):
return ", ".join(f"{x:.2f}" for x in lst)
delta_coords_astro = [delta_lat, delta_lon]
delta_coords_geo = [alexandria_coords[0] - aswan_coords[0], alexandria_coords[1] - aswan_coords[1]]
console.print(f"Delta coordenadas astronômicas: {format_list(delta_coords_astro)}")
console.print(f"Delta coordenadas geográficas: {format_list(delta_coords_geo)}")Loading...
Correções ao Experimento¶
Precisamos considerar que:
- ‼️O tamanho da sombra em Aswan não é zero, sua latitude não é no trópico de câncer.
- ‼️A longitude das cidades não é a mesma.
Para dois pontos na esfera, a distância entre eles é dada pela fórmula de Haversine
A diferença de longitude é a diferença de tempo para as passagens no meridiano, convertida em horas. Falta apenas calcular o tempo em Alexandria.
Não temos como saber as coordenadas exatas, vamos colocar a origem em Alexandra e determinar as coordenadas relativas de Aswan:
lat_alexandria, lon_alexandria = (0, 0)
lat_aswan, lon_aswan = (delta_lat, delta_lon)
R_terra_corrected = great_circle_distance / (2 * np.arcsin( np.sqrt( np.sin(np.radians((lat_alexandria - lat_aswan) / 2))**2 + np.cos(np.radians(lat_alexandria)) * np.cos(np.radians(lat_aswan)) * np.sin(np.radians((lon_alexandria - lon_aswan) / 2))**2)))Source
import astropy.constants as const
R_terra_earth = const.R_earth.value / 1000 # Convertendo para km
results = Table(title="Raio da Terra")
results.add_column("Grandezas", justify="right", style="cyan", no_wrap=True)
results.add_column("Valor", justify="left", style="yellow", no_wrap=True)
results.add_row("Raio da Terra (Eratóstenes)", f"{R_terra:.2f} km")
results.add_row("Correção de Lat/Lon", f"{R_terra_corrected:.2f} km")
results.add_row("Valor WSG84", f"{R_terra_earth:.2f} km")
results.add_row("Diferença (Corrigido - Nominal)", f"{R_terra_corrected - R_terra_earth:.2f} km")
results.add_row("Diferença (Eratostenes - Nominal)", f"{R_terra - R_terra_earth:.2f} km")
results.add_row("Diferença porcentual (corrigido)", f"{((R_terra_corrected - R_terra_earth) / R_terra_earth) * 100:.2f}%")
results.add_row("Diferença porcentual (Eratostenes)", f"{((R_terra - R_terra_earth) / R_terra_earth) * 100:.2f}%")
console.print(results)Loading...