Tamanho Angular do Sol e da Lua¶
Source
from src.astroufcg.astronomy import setup, make_observer
from src.astroufcg.grecia import aristarco
from PIL import Image
import numpy as np
from sunpy.net import Fido
from sunpy.net import attrs as a
import sunpy.map
import sunpy
import matplotlib.pyplot as plt
import astropy.units as u
import copy
from sunpy.map import make_fitswcs_header
from sunpy.time import parse_time
from sunpy.coordinates import Helioprojective, sun
from astropy.coordinates import EarthLocation
from astropy.coordinates import SkyCoordNa imagem da eclipse solar fazemos o seguinte processamento#:
- Equalização de Histograma para evidenciar nuances de intensidade.
- Desfoque gaussiano para eliminar pontas e arestas que dificultam a determinação de contornos.
- Transformamos a imagem em uma máscara binária.
- Aplicamos um algoritmo que determina os contornos existentes na imagem.
- Para cada contorno fazemos um ajste de mínimos quadrados para um círculo.
from PIL import Image
SAMPLE_PHOTO = "../../../data/eclipse/total_solar_eclipse2017.jpg"
tags = aristarco.read_exif(SAMPLE_PHOTO)
moon_image = Image.open(SAMPLE_PHOTO).convert("L")
moon_image = moon_image.transpose(Image.FLIP_TOP_BOTTOM)
moon_data = np.array(moon_image)
results_moon, ax_moon, fig_moon = aristarco.get_disk(moon_data, plot=True)
result_moon = results_moon[np.vstack(results_moon)[:, 0].argmin()]
Vamos repetir o procedimento para uma imagem científica, no formato FITs, que contém informações sobre as coordenadas.
aia_result = Fido.search(
a.Time("2017-08-21 17:27:00", "2017-08-21 17:45:00"),
a.Instrument("AIA"),
a.Wavelength(171 * u.Angstrom),
)
files = Fido.fetch(aia_result[0, 0], site="NSO", path="../../../data/eclipse/")
aia_map = sunpy.map.Map(files[0])
fig, ax = plt.subplots(figsize=(5, 5), subplot_kw={"projection": aia_map})
aia_map.plot(axes=ax, autoalign=True)
aia_map.draw_grid(axes=ax)
plt.show()results_aia, ax_aia, fig_aia = aristarco.get_disk(aia_map.data, sigma=171, plot=True)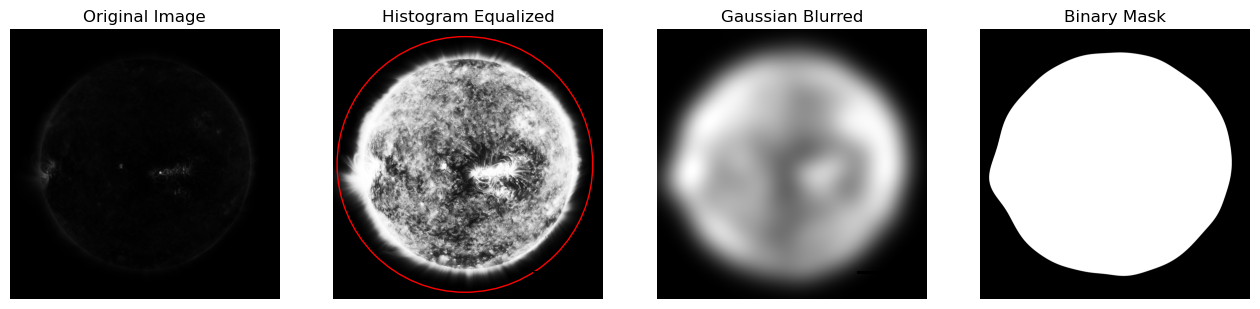
Esta imagem contém dados suficientes para a determinação do diâmetro angular da Lua. A partir da plate scale do mapa e do tamanho a lua em pixels.
half_moon_angular = u.Quantity(aia_map.scale) * results_aia[0][0] * u.pix
print(f"Diâmetro angular da Lua: {(2 * half_moon_angular).to(u.deg)}")
# Determinando plate_scale da imagem da Lua
moon_scale = (
u.Quantity(aia_map.scale) * results_aia[0][0] / result_moon[0]
)
# Construção do cabeçalho FITS
# Observador
loc = EarthLocation(
lat=tags["lat"],
lon=tags["lon"],
height=0,
)
observer = loc.get_itrs(parse_time(tags["time"]))
frame = sunpy.coordinates.Helioprojective(
observer=observer, obstime=parse_time(tags["time"])
)
moon_coord = SkyCoord(
sunpy.coordinates.get_body_heliographic_stonyhurst(
"moon", parse_time(tags["time"]), observer=observer))
solar_rotation_angle = sun.orientation(loc, parse_time(tags["time"]))
moon_hpc = moon_coord.transform_to(frame)
center_pix = results_moon[1].astype(int)[1:]
# Aplicamos uma máscara para tornar o fundo transparente
moon_data = copy.deepcopy(moon_data)
moon_data[moon_data < 30] = False # Ajuste o valor conforme
header_moon = make_fitswcs_header(
moon_data,
moon_hpc,
reference_pixel=u.Quantity(center_pix, unit="pixel"),
scale=moon_scale,
rotation_angle=solar_rotation_angle,
exposure=tags["exposure_time"],
instrument=tags["camera_model"],
observatory=tags["author"],
)
eclipse_map = sunpy.map.Map(moon_data, header_moon)Diâmetro angular da Lua: [0.64681687 0.64681687] deg
2025-07-19 16:49:33 - sunpy - INFO: Apparent body location accounts for 1.23 seconds of light travel time
INFO: Apparent body location accounts for 1.23 seconds of light travel time [sunpy.coordinates.ephemeris]
fig = plt.figure(figsize=(10, 15))
ax = plt.subplot(projection=eclipse_map)
# Set the axes background to black.
ax.set_facecolor("k")
# Plot the AIA image.
aia_map.plot()
# Plot the eclipse image
eclipse_map.plot()
# Draw heliographic and helioprojective grids
eclipse_map.draw_grid()
ax.coords.grid(color="lightgray", alpha=0.7, linewidth=.5)2025-07-19 16:49:33 - sunpy - INFO: Using mesh-based autoalignment
INFO: Using mesh-based autoalignment [sunpy.map.mapbase]

Geometria da Experiência¶
Source
import pyvista as pv
from pyvista import examples
import astropy.constants as const
from skyfield import almanac
from src.astroufcg.astronomy import setup
import pandas as pd
import osmnx as ox
pv.set_jupyter_backend('trame')
import warnings
warnings.filterwarnings('ignore', category=UserWarning)Source
from src.astroufcg.astronomy import ts, eph, lua, terra, sol, make_observerstart = ts.ut1(-200, 1, 1)
end = ts.ut1(-200, 12, 31)
t, y = almanac.find_discrete(start, end, almanac.moon_phases(eph))
date = [time for time, phase in zip(t, y) if phase == 1][0]
site_01 = "Alexandria, Egypt"
location = pd.DataFrame([list(ox.geocode(site_01))], columns=["lat", "lon"]).iloc[0]
observer = make_observer(location)
moon_obs = observer.at(date).observe(lua)
sun_obs = observer.at(date).observe(sol)
ra_moon, dec_moon, distance_moon = moon_obs.radec()
ra_sun, dec_sun, distance_sun = sun_obs.radec()
R_moon = distance_moon.to(u.km) * np.sin(np.radians(half_moon_angular[0].to(u.rad)))
R_sun = distance_sun.to(u.km) * np.sin(np.radians(half_moon_angular[0].to(u.rad)))
R_earth = const.R_earth# Tamanhos para o modelo
_Rt = 1
_angle = np.radians(80)
_R_sun = (R_sun / R_earth).decompose()
_R_moon = (R_moon / R_earth).decompose()
_Ds = 30 * _Rt
_Rs, _Rm = 2 * _Rt, 0.8 * _Rt
_Dm = _Ds * np.cos(_angle)
_Pt, _Ps, _Pm = (0, 0, 0), (_Ds, 0, 0), (_Dm * np.cos(_angle), _Dm * np.sin(_angle), 0)_terra, _sol, _lua = [pv.Sphere(radius=_R, center=_P, theta_resolution=100, phi_resolution=100) for _R, _P in zip([_Rt, _Rs, _Rm], [_Pt, _Ps, _Pm])]
_terra.texture_map_to_sphere(inplace=True)
_sol.texture_map_to_sphere(inplace=True)
_lua.texture_map_to_sphere(inplace=True)
moon_texture = pv.Texture("../../../data/textures/2k_moon.jpg")
sun_texture = pv.Texture("../../../data/textures/2k_sun.jpg")
earth_texture = examples.load_globe_texture()
lines = pv.MultipleLines(np.array([_Pt, _Ps, _Ps, _Pm, _Pm, _Pt]))
sun_light = pv.Light(
position=(_Ds - _Rs, 0, 0),
focal_point=_Pm,
intensity=50,
color="lightgray",
positional=True,
cone_angle=30,
shadow_attenuation=0.3,
)
ambient_light = pv.Light(
position=(-_Ds / 2, 0, 0),
focal_point=_Pm,
intensity=5,
color="lightgray",
positional=True,
cone_angle=60,
shadow_attenuation=0.3,
)pl = pv.Plotter(notebook=True, lighting="three lights", polygon_smoothing=True, window_size=[1000, 400])
pl.add_mesh(lines, color="maroon", line_width=5)
pl.add_light(sun_light)
pl.add_light(ambient_light)
pl.set_background("black")
pl.add_mesh(
_terra, texture=earth_texture, smooth_shading=True, ambient=0.8, diffuse=0.5
)
pl.add_mesh(_sol, texture=sun_texture, smooth_shading=True, opacity=0.6)
pl.add_mesh(
_lua,
texture=moon_texture,
smooth_shading=True,
ambient=0.8,
diffuse=0.5,
)
pl.enable_anti_aliasing("fxaa")
pl.enable_eye_dome_lighting()
pl.camera_position = "xy"
pl.camera.azimuth = 180
pl.camera.zoom(2)
pl.save_graphic("../../00_images/cap_01/lua_solar_eclipse.svg")
pl.show(jupyter_backend="trame")
2025-07-19 16:51:48 - wslink.backends.aiohttp - INFO: client 4e3a4cf374ca4e41b3fa1c7d1b495206 disconnected
2025-07-19 16:51:48 - wslink.backends.aiohttp - INFO: No more connections, scheduling shutdown
2025-07-19 16:51:48 - aiohttp.access - INFO: 127.0.0.1 [19/Jul/2025:16:51:39 -0300] "GET /ws HTTP/1.1" 101 0 "-" "Mozilla/5.0 (X11; Linux x86_64) AppleWebKit/537.36 (KHTML, like Gecko) Code/1.101.2 Chrome/134.0.6998.205 Electron/35.5.1 Safari/537.36"
Figure 1:Geometria para a experiência de Aristarco. Na figura as distâncias não são proporcionais para evidenciar or ângulos. Durante a meia-lua, o ângulo com a Lua no vértice é e precisamos medir o ângulo com a Terra no vértice.
Fazendo a Observação da meia Lua¶
Agora nós vamos implementar esta observação utilizando o Skyfield. Para fazer o gráfico em coordenadas esféricas eu vou aproveitar os recursos de WCS do astropy.
- Definimos um WCS com projeção zenital.
- Baixamos dados de constelações
- Criamos uma lista com as constelações do zodíaco.
- Acessamos o catálogo Hipparco no serviço Vizier para obter as posições das estrelas do céu com magnitude inferior 6.
- Construimos as posições do Sol e da Lua para o dia de lua quarto crescente.
- Construímos as posições das estrelas levando em conta a precessão dos equinócios.
- Sobrepomos a eclíptica e o equador celeste.
- Fazemos um gráfico do céu.
from skyfield.api import (
load,
Loader,
Star,
load_constellation_map,
load_constellation_names,
)
from skyfield.data import stellarium
from astropy.coordinates import Angle, SkyCoord
from astropy.wcs import WCS
from astropy import units as u
import numpy as np
import pandas as pd
# Cria um WCS para projeção estereográfica (AZP)
wcs = WCS(naxis=2)
wcs.wcs.ctype = ["AZP-SIN", "AZP-SIN"] # Projeção azimutal estereográfica
wcs.wcs.crpix = [512, 512] # Centro da imagem (pixel reference)
wcs.wcs.crval = [0, 90] # Centro em Az=0°, Alt=90° (zênite)
wcs.wcs.cdelt = [-0.1, 0.1] # Escala em graus/pixel
wcs.wcs.cunit = ["deg", "deg"]
# (Opcional) Configura parâmetros específicos da projeção AZP
wcs.wcs.set_pv([(2, 1, 45)]) # Ângulo de projeção (45° para estereográfica)
const_dict = dict(load_constellation_names())
constellation_at = load_constellation_map()
url = (
"https://raw.githubusercontent.com/Stellarium/stellarium/"
"eb47095a9282cf6b981f6e37fe1ea3a3ae0fd167"
"/skycultures/modern_st/constellationship.fab"
)
load = Loader("../../../data/skyfield")
with load.open(url) as f:
constellations = stellarium.parse_constellations(f)
edges = [edge for name, edges in constellations for edge in edges]
edges_star1 = [star1 for star1, star2 in edges]
edges_star2 = [star2 for star1, star2 in edges]
zodiac_abbrv = [
"Ari",
"Tau",
"Gem",
"Cnc",
"Leo",
"Vir",
"Lib",
"Sco",
"Sgr",
"Cap",
"Aqr",
"Psc",
]
from astroquery.vizier import Vizier
Vizier.clear_cache()
catalog = "I/239/hip_main"
vizier = Vizier(
columns=["HIP", "_RA.icrs", "_DE.icrs", "Vmag", "Plx", "pmRA", "pmDE"],
catalog=catalog,
column_filters={"Vmag": "<=5.0"},
)
vizier.ROW_LIMIT = -1obs_lua = observer.at(date).observe(lua)
lua_Alt, lua_Az, _ = obs_lua.apparent().altaz()
obs_sol = observer.at(date).observe(sol).apparent()
sol_Alt, sol_Az, _ = obs_sol.altaz()
lua_pixel = wcs.world_to_pixel(lua_Az.degrees * u.deg, lua_Alt.degrees * u.deg)
sol_pixel = wcs.world_to_pixel(sol_Az.degrees * u.deg, sol_Alt.degrees * u.deg)hipparcos = vizier.query_constraints()[0].to_pandas()
hipparcos["ra_hours"] = Angle(hipparcos["_RA.icrs"], unit=u.hourangle).hour
hipparcos["dec_degrees"] = hipparcos["_DE.icrs"]
hipparcos["epoch_year"] = 2000.0
_start_csts = np.concatenate([np.array(const[1]).ravel() for const in constellations])
_csts_names = np.concatenate(
[np.array([const[0]] * 2 * len(const[1])) for const in constellations]
)
df_csts = pd.DataFrame(
{
"HIP": _start_csts,
"cst": _csts_names,
}
)
df_csts = df_csts.drop_duplicates(subset="HIP").set_index("HIP")
df = hipparcos.copy()
limiting_magnitude = 5.0
all_stars = Star.from_dataframe(df)
stars = observer.at(date).observe(all_stars)
Alt, Az, _ = stars.apparent().altaz()
_RA, _DEC, _ = stars.radec(epoch=date)
var_names = ["Alt", "Az", "RA", "DEC"]
for varname, var in zip(var_names, [Alt, Az, _RA, _DEC]):
df[varname] = var.degrees
df = df.set_index("HIP")
df = df.join(df_csts, how="left")
df["x"], df["y"] = wcs.world_to_pixel(df.Az.values * u.deg, df.Alt.values * u.deg)from astropy.time import TimeDelta
from skyfield.positionlib import Apparent
ra_hours = np.arange(-48, 48, 0.1)
interval = ts.from_astropy(date.to_astropy() + np.arange(300) * TimeDelta(5 * u.min))
obs_ecliptic = observer.at(interval).observe(sol).apparent()
alt_ecliptic, az_ecliptic, _ = obs_ecliptic.altaz()
fake_star = Star(
ra_hours=ra_hours * u.hourangle, dec_degrees=np.zeros_like(ra_hours) * u.deg
)
obs_equatorial = observer.at(date).observe(fake_star).apparent()
equatorial_alt, equatorial_az, _ = obs_equatorial.altaz()import matplotlib.pyplot as plt
import numpy as np
import matplotlib as mpl
n_colors = len(zodiac_abbrv) # Number of colors to generate
colormap_name = "plasma" # Choose a colormap
cmap = mpl.colormaps[colormap_name]
color_positions = np.linspace(0, 1, n_colors)
colors = cmap(color_positions)
def get_size(magnitude):
"""Calculate the size of the star based on its magnitude."""
return 20 * (6 - magnitude) / 6
fig, ax = plt.subplots(figsize=(16, 9), subplot_kw=dict(projection=wcs))
ax.set_facecolor("black")
Az = ax.coords[0]
Alt = ax.coords[1]
Az.set_axislabel("Azimuth (degrees)")
Alt.set_axislabel("Altitude (degrees)")
ax.coords.grid(color="lightgray", alpha=0.5, linestyle="solid")
ax.plot(*wcs.wcs_world2pix(az_ecliptic.degrees, alt_ecliptic.degrees, 0), color="yellow", label="Ecliptic")
ax.plot(*wcs.wcs_world2pix(equatorial_az.degrees, equatorial_alt.degrees, 0), color="cyan", label="Equatorial")
zodiac = df[df.cst.isin(zodiac_abbrv)].groupby("cst")
for cst, group in zodiac:
ax.text(
group.iloc[0, :].x,
group.iloc[0, :].y,
cst,
color="red",
fontsize=12,
ha="center",
va="center",
)
ax.scatter(
group.x.values,
group.y.values,
s=2 * get_size(group.Vmag.values),
c=colors[zodiac_abbrv.index(cst)],
marker="*",
label=cst,
alpha=0.5,
)
ax.scatter(
*lua_pixel,
s=200,
c="midnightblue",
marker="o",
label="Lua",
)
ax.scatter(
*sol_pixel,
s=200,
c="gold",
marker="o",
label="Sol",
)
plt.show()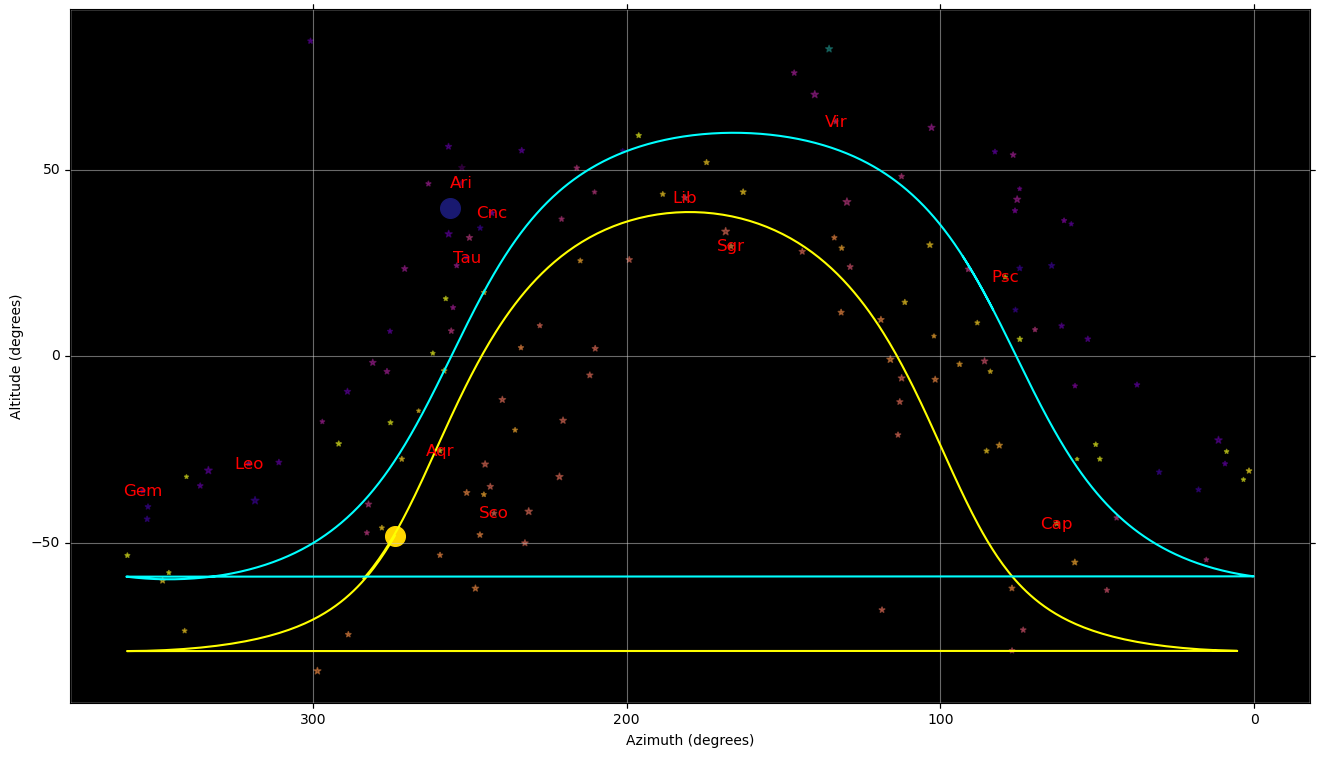
Analisando os Resultados¶
Para obter os ângulos entre os planetas podemos utilizar as posições como coordenadas cartesianas e construir os ângulos com a lei dos cossenos.
interval = ts.from_astropy(date.to_astropy() + np.arange(-10, 10) * TimeDelta(5 * u.min))
# Obter posições relativas no sistema baricêntrico
pos_earth = terra.at(interval).position.km
pos_moon = lua.at(interval).position.km
pos_sun = sol.at(interval).position.km
# Vetores entre os corpos (para formar o triângulo)
vec_TE = pos_earth - pos_moon # Terra ← Lua
vec_SE = pos_earth - pos_sun # Terra ← Sol
vec_SM = pos_moon - pos_sun # Lua ← Sol
# Normas dos vetores (lados do triângulo)
a = np.linalg.norm(vec_SM, axis=0) # lado oposto ao vértice Terra
b = np.linalg.norm(vec_SE, axis=0) # lado oposto ao vértice Lua
c = np.linalg.norm(vec_TE, axis=0) # lado oposto ao vértice Sol
# Função para calcular ângulo a partir da Lei dos Cossenos
def law_of_cosines(a, b, c):
return np.arccos((b**2 + c**2 - a**2) / (2 * b * c))
# Ângulos internos (em radianos)
angle_Terra = law_of_cosines(a, b, c)
angle_Lua = law_of_cosines(b, c, a)
angle_Sol = law_of_cosines(c, a, b)idx = (np.degrees(angle_Lua)>=90).argmin()
t_halfmoon = interval[idx]
delta_t = (t_halfmoon.to_astropy() - date.to_astropy()).to(u.min)
theta_almanac = np.degrees(angle_Terra[10])
theta_halfmoon = np.degrees(angle_Terra[idx])Aqui surge uma questão interessante, a data indicada na rotina almanac esta um pouco defasada:
print("Horário do meio da Lua Quarto Crescente:", date.ut1_strftime("%Y-%m-%d %H:%M:%S"))
print(f"Horário em que a Lua está a 90° do Sol: {t_halfmoon.ut1_strftime('%Y-%m-%d %H:%M:%S')}")
print(f"ângulo na data almanac $\hat\{{Terra\}}$: {theta_almanac:.2f}")
print(f"ângulo em 90° $\hat\{{Terra\}}$: {theta_halfmoon:.2f}")Horário do meio da Lua Quarto Crescente: -200-01-19 19:15:50
Horário em que a Lua está a 90° do Sol: -200-01-19 18:55:50
ângulo na data almanac $\hat\{Terra\}$: 89.99
ângulo em 90° $\hat\{Terra\}$: 89.84
from IPython.display import display, Math, Latex
display(Math(r"\Delta t = " + f"{delta_t.to(u.min):.2f}"))
display(Latex(f"$$ \\frac{{R_{{\odot}}}}{{R_{{moon}}}} = {1/np.cos(np.radians(theta_almanac)):.2f}$$"))
display(
Latex(
f"$$ \\frac{{R_{{\odot}}}}{{R_{{moon}}}} = {1 / np.cos(np.radians(theta_halfmoon)):.2f}$$"
)
)Vinte minutos de diferença e poderíamos errar por duas ordens de grandeza. Note que é necessário medir um ângulo, com precisão, na ordem de 0.5 minutos de arco. O ângulo entre dois objetos que sequer estão no céu ao mesmo tempo!!